The abbreviation of RSA is Rivest–Shamir–Adleman, which is the name of three people.Rivest along with Shamir and Adleman are the inventors of the RSA algorithm.
How does RSA work?
An RSA user creates and publishes a public key based on two large prime numbers, along with an auxiliary value. The prime numbers are kept secret. Messages can be encrypted by anyone, via the public key, but can only be decoded by someone who knows the prime numbers.
Generator the Private key:
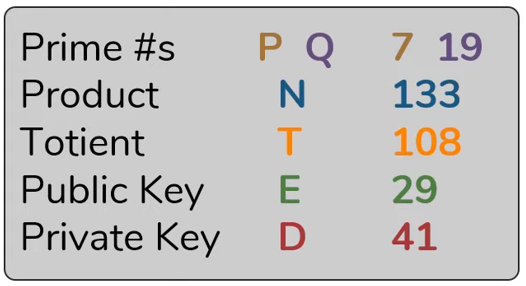
- Choose 2 prime numbers P and Q
- Calculate the product of these two prime numbers (P*Q)
- Calculate totient: T = (P-1)*(Q-1)
- To select a public key (E), the following three conditions must be met:
- The public key must be a prime number
- The public key must be less than totient
- The public key cannot be a factor of totient
- To select a private key (D), the following conditions must be met:
- The product of D and E modulo T must equal 1: (D*E) MOD T = 1
- The product of D and E modulo T must equal 1: (D*E) MOD T = 1
The process of Encryption and Decryption:
Encryption: Message^E MOD N = Cipher
Decryption: Cipher^D MOD N = Message
Encryption: (60 ^ 29) MOD 133 = 86
Decryption: (86 ^ 41) MOD 133 = 60
My example code on Python:
import random
prime_number = [307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
prime_p = random.choice(prime_number)
prime_q = random.choice(prime_number)
product_n = prime_p * prime_q
totient_t = (prime_p - 1) * (prime_q - 1)
for number in prime_number:
if totient_t % number != 0:
public_key = number
break
n = 1
flag = True
while flag:
if (totient_t * n + 1) % public_key != 0:
n += 1
else:
private_key = int((totient_t * n + 1) / public_key)
flag = False
print(prime_p, prime_q, product_n, totient_t, public_key, private_key)
def encode(public_key, message, product_n):
encode = (message ** public_key) % product_n
return(encode)
def decode(private_key, product_n, encode):
decode_message = (encode ** private_key) % product_n
return(decode_message)
direction = input("Type 'encode' to encrypt, type 'decode' to decrypt:\n")
if direction == "encode":
message = int(input("What massage do you want to encode?\n"))
print(f"Your public key is {public_key} and the product_N is {product_n}.")
print(f"Your encoded message is {encode(public_key, message, product_n)}")
if direction == "decode":
encode = int(input("What massage do you want to decode?\n"))
user_private_key = int(input("What is your private key?\n"))
user_product_n = int(input("What is your product_N?\n"))
print(f"Your encoded message is {decode(user_private_key, user_product_n, encode)}")RSA Encryption Algorithm