History of Boolean Algebra
Around the 1850s, a British mathematician, George Boole developed a new form of mathematics that is now known as Boolean Algebra. His intention was to use mathematical techniques to represent and test logical and philosophical arguments. However, his work found little application outside the school of symbolic logic for almost one hundred years. Until the late 1930s, a graduate student Claude Elwood Shannon showed that Boolean Algebra offered an ideal technique for representing the logical operation of digital systems.
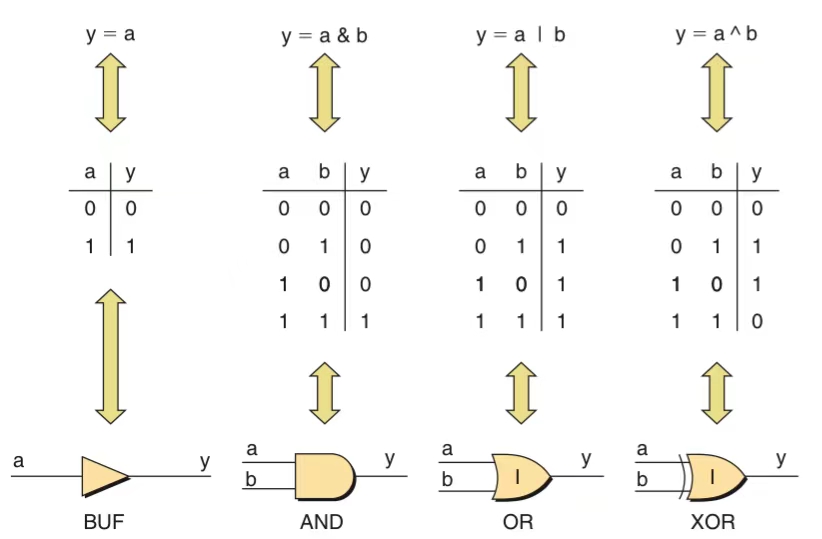
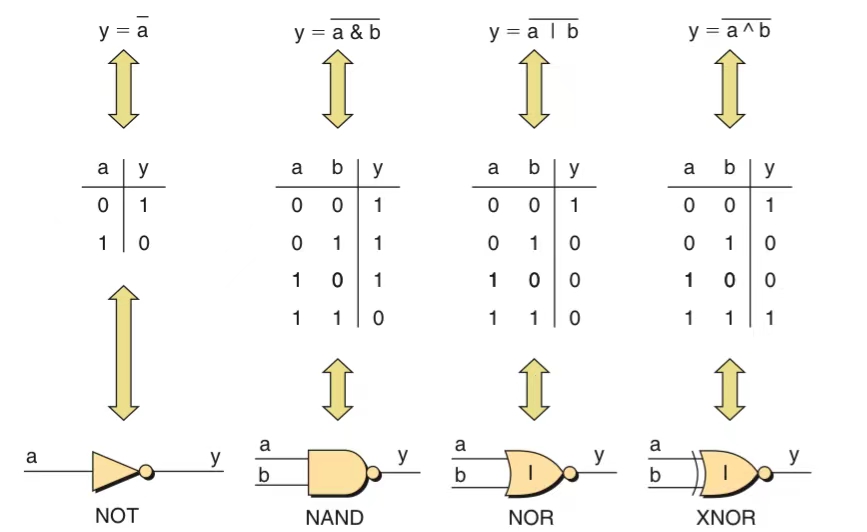
Primitive Logic Functions
Logical functions can be represented using graphical symbols, equations or truth tables and these views can be used interchangeably.
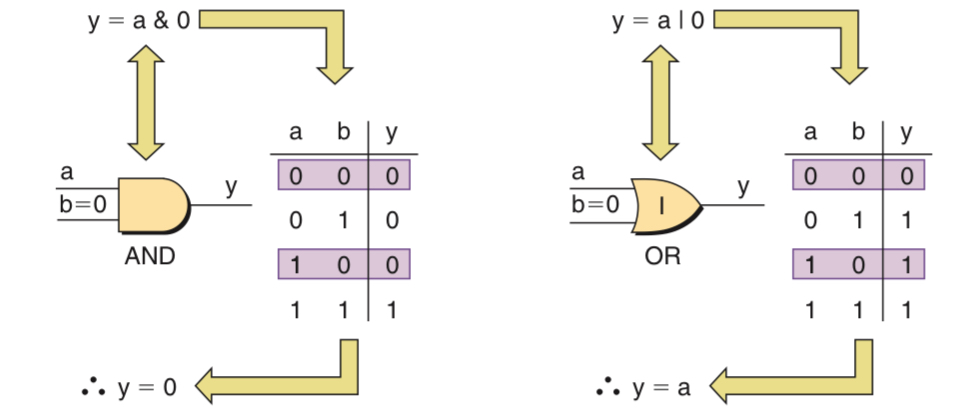
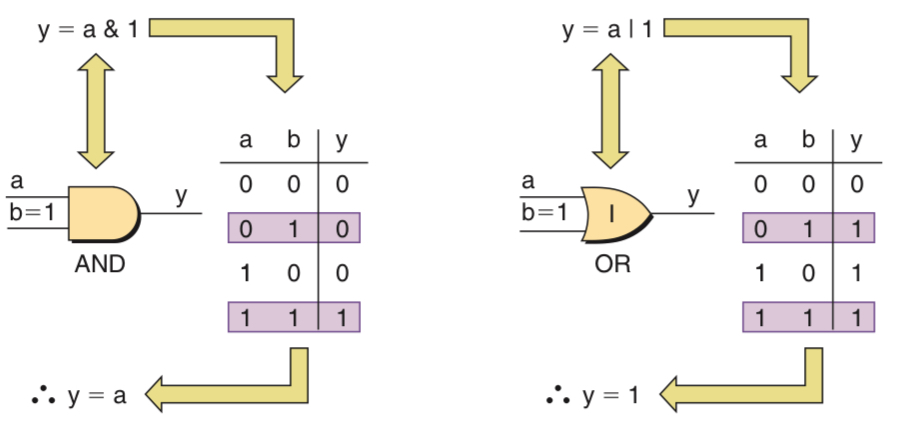
Combining Variable with Logic 0 Or 1
The input to a gate can not only be a variable but also can be 0 or 1.
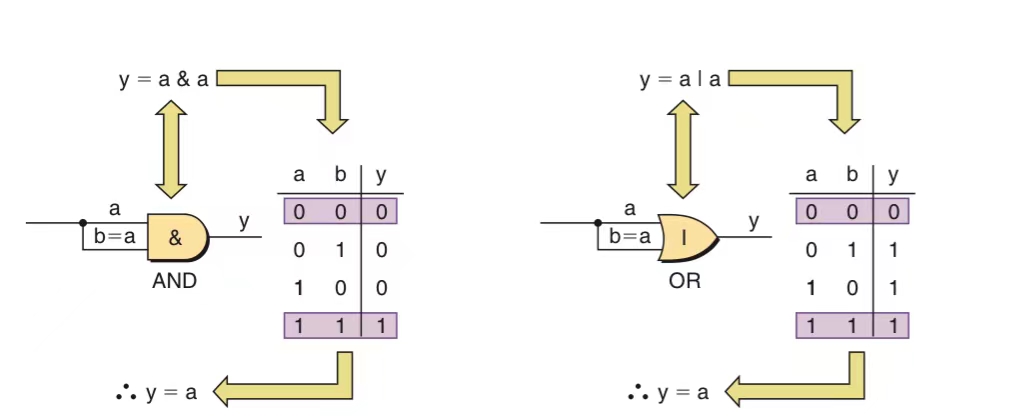
Idempotent Rule
This law state that repeating the same operation on a Boolean variable results in the same value as the original variable.
- Idempotent Law for AND: A & A = A
- Idempotent Law for OR: A | A = A
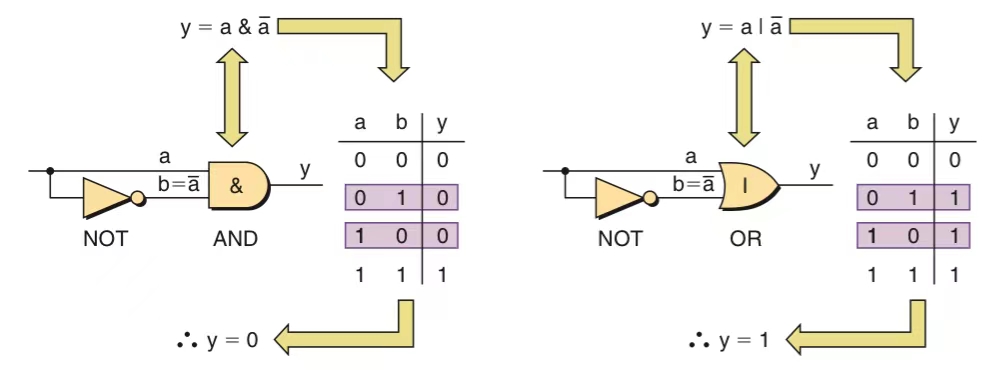
Complementary Rule
This law state that a Boolean variable ORed with its complement is always true (1), and a Boolean variable ANDed with its complement is always false (0)
- Complementary Law for OR: A | Ā = 1
- Complementary Law for AND: A & Ā = 0
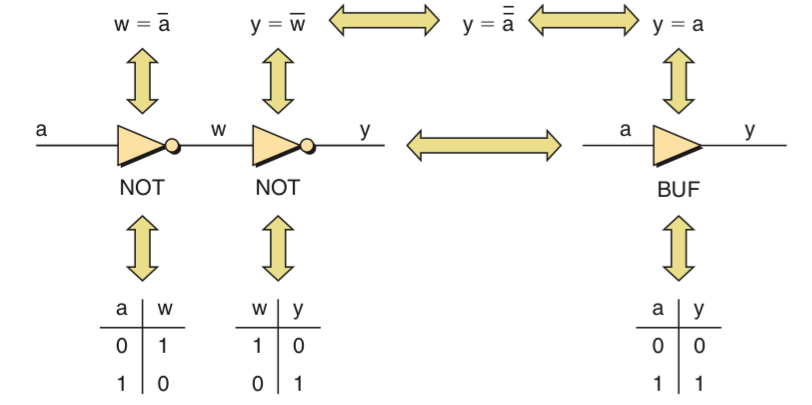
Involution Rule
This law states that an even number of inversions cancel each other out, for example, two NOT functions connected in series generate an identical result to that of a BUF function.
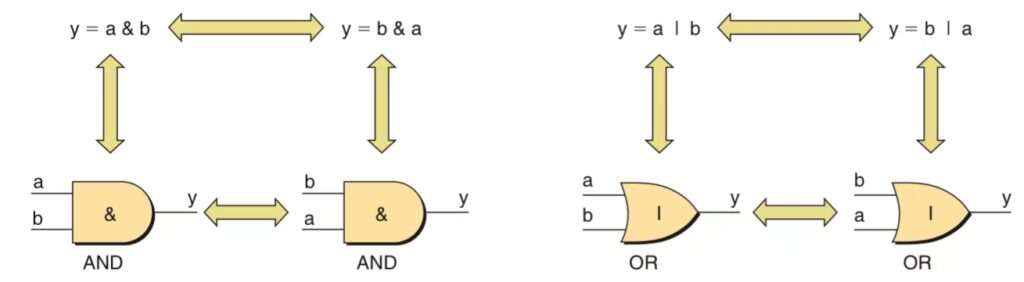
The Commutative Rule
This law states that the order in which variables are specified will not affect the result of an AND or OR operation.
The Associative Rule
This law states that the order in which pairs of variables are associated together will not affect the result of multiple AND or OR operations.
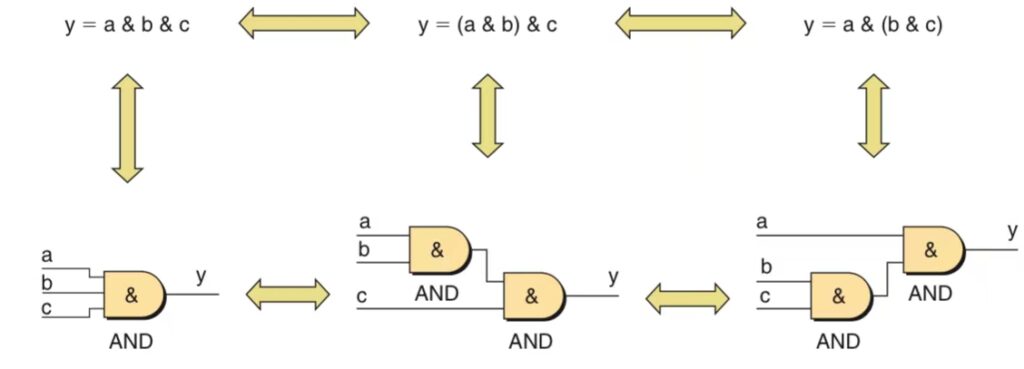
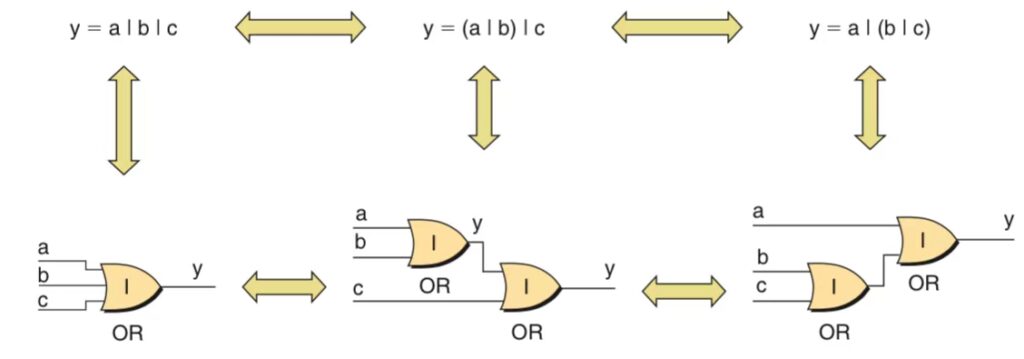
Precedence of Operation
In standard arithmetic, the multiplication operator is said to have a higher precedence than the addition operator. This means that, if an equation contains both multiplication and addition operators without parenthesis, then the multiplication is performed before the addition. Similarly, in Boolean Algebra, the & (AND) operator has a higher precedence than the | (OR) operator.
Due to the similarities between the arithmetic and logical operators, the & (AND) operator is known as a logical multiplication or product, while the | (OR) operator is known as a logical addition or sum.
E.g. a | b & c ≡ a | (b & c)
First Distributive Rule
In standard arithmetic, the multiplication operator will distribute over the addition operator because it has a higher precedence.
E.g. 6 ⋅ (5 + 2) ≡ 6 ⋅ 5 + 6 ⋅ 2
Similarly, in Boolean Algebra, the & (AND) operator will distribute over an | (OR) operator because it has a higher precedence.
E.g. a & (b | c) ≡ (a & b) | (a & c)
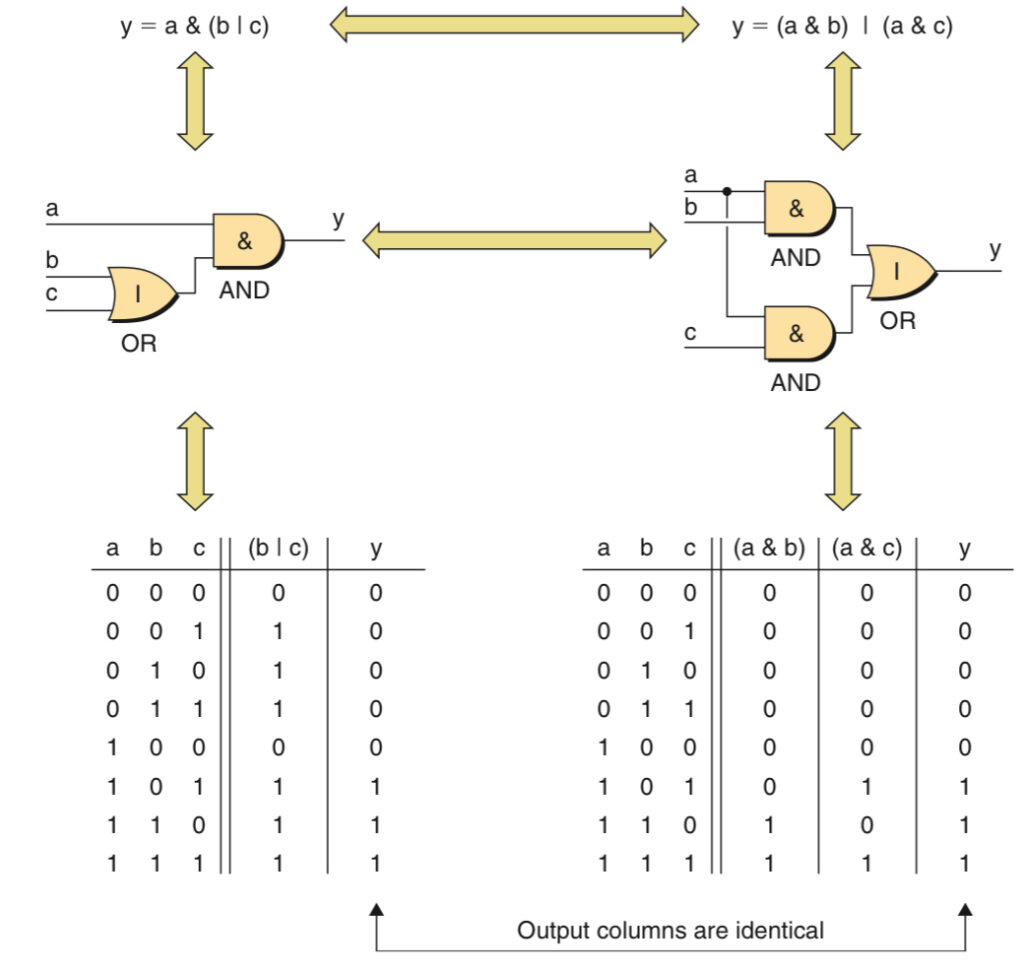
Second Distributive Rule
In standard arithmetic, the addition operator will not distribute over the multiplication operator because it has a lower precedence.
E.g. 6 + (5 ⋅ 2) ≠ (6 + 5) ⋅ (6 + 2)
However, in Boolean Algebra even though the | (OR)operator has lower precedence than the & (AND) ,o it will still distribute ver the & operator.
E.g. a | (b & c) ≡ (a | b) & (a | c)
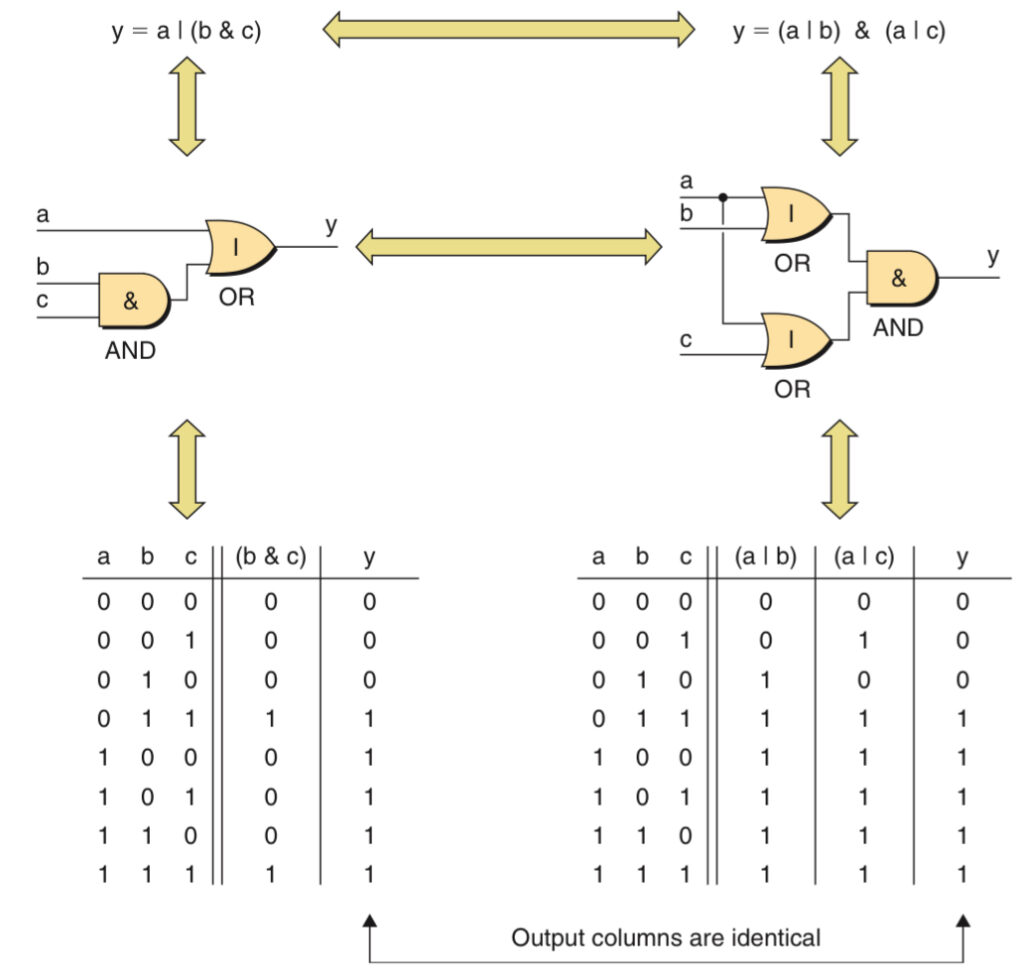
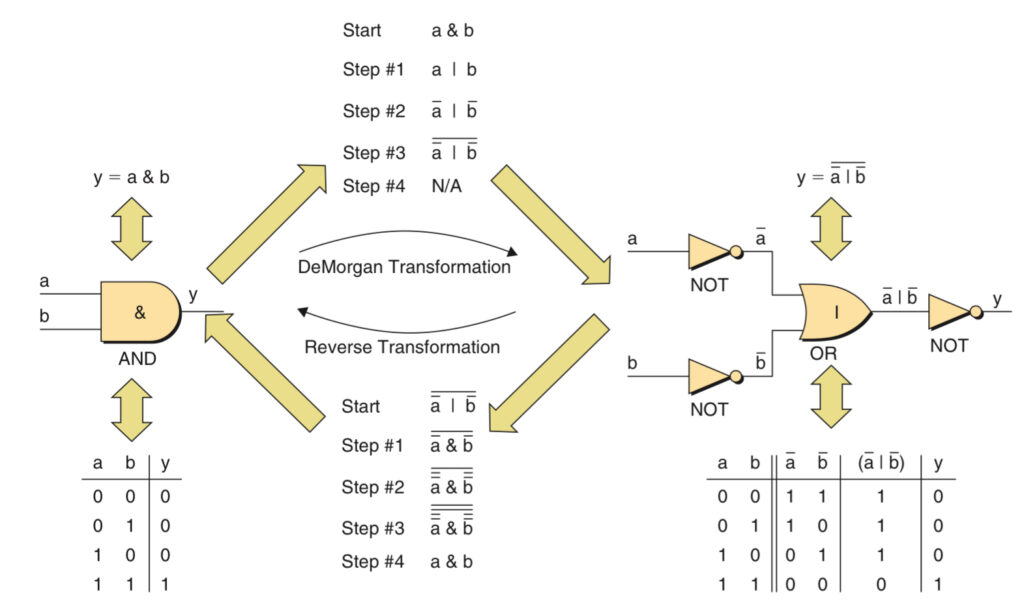
DeMorgan Transformation
DeMorgan transformation is a set of rules which facilitate the conversion of Boolean expressions into alternate and often more convenient forms.
A deMorgan Transformation comprises four steps:
- Exchange all of the & operators for | operators and vice versa.
- Invert all the variables, also exchange 0s for 1s and vice versa
- Invert the entire function
- Reduce any multiple inversions.
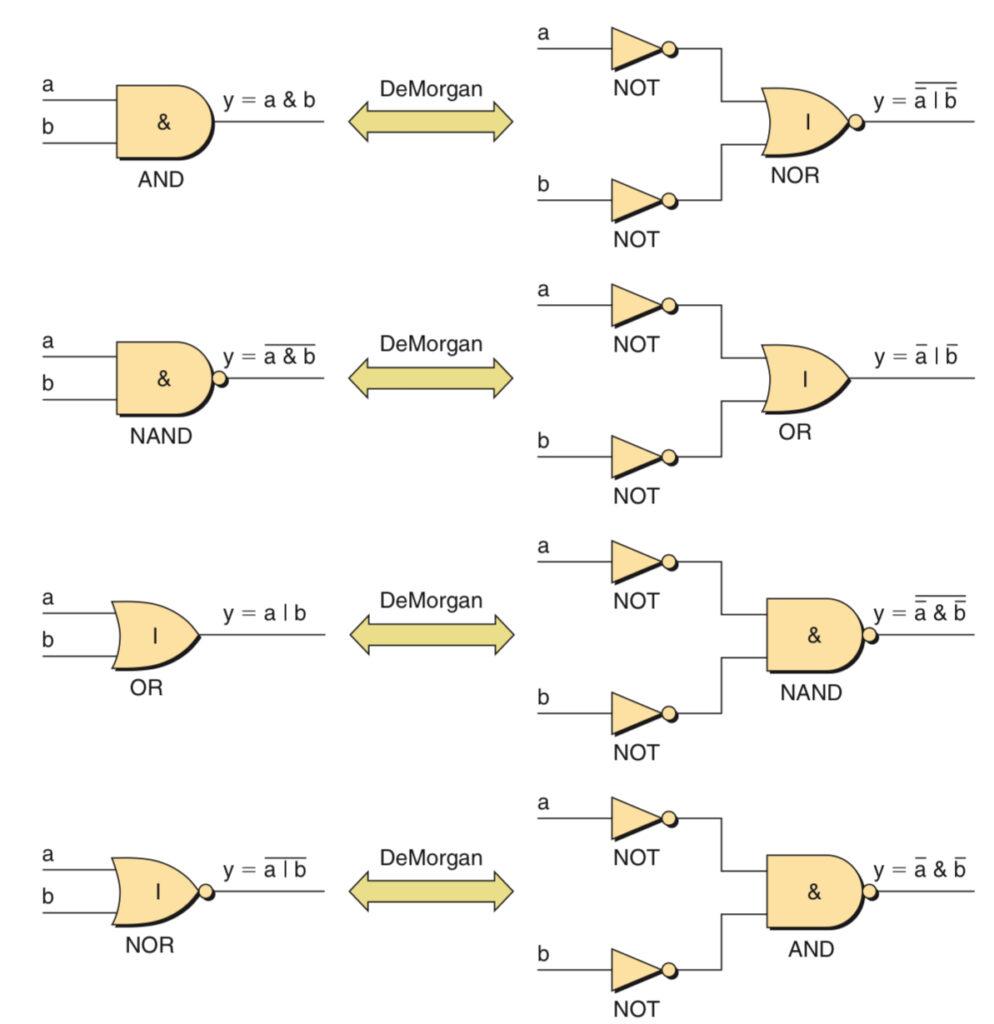
DeMorgan Transformation for AND, OR, NAND, and NOR functions:
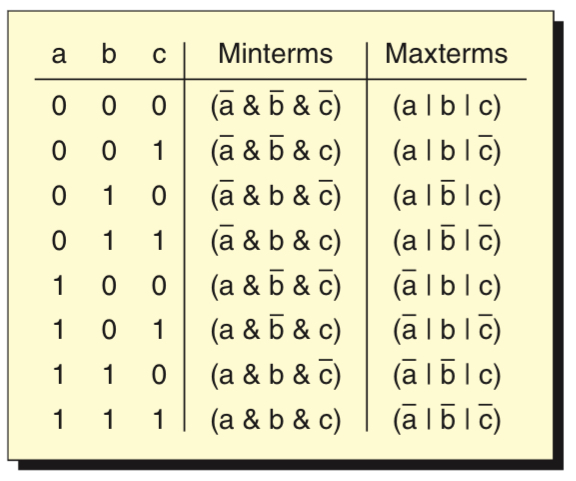
Minterms & Maxterms
A minterm is a product (AND operation) of all the variables in the function, where each variable appears in true or complemented form. A minterm corresponds to a unique row in a truth table where the function is true (1).
A maxterm is a sum (OR operation) of all the variables in the function, where each variable appears in true or complemented form. A maxterm corresponds to a unique row in a truth table where the function is false (0).
Sum of Products VS Product of Sums
There are two commonly used techniques for deriving Boolean equations from truth table. In the first technique, the minterms corresponding to each line in the truth table for which the output is logic 1 are extracted and combined using | (OR) operators. In the second technique, the maxterms corresponding to each line in the truth table for which the output is a logic 0 are combined using & (AND) operators.
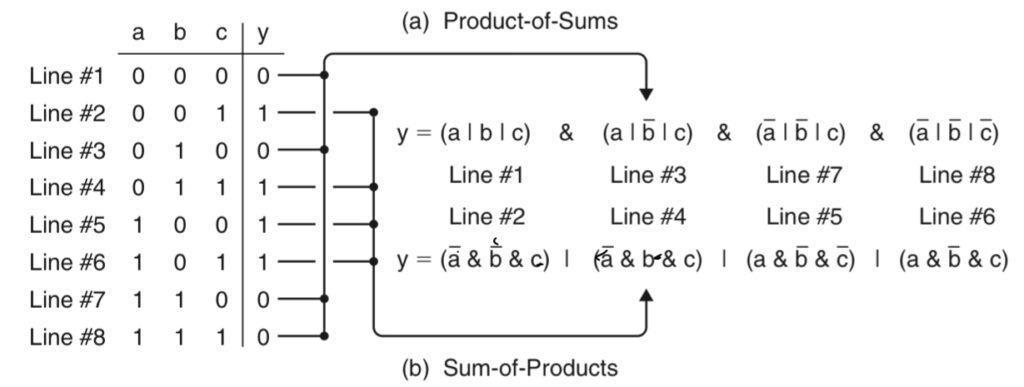
The sum of products and the product of sums forms complement each other and return identical results. Once an equation has been obtained in the required form, the designer would typically make use of the appropriate implications rules to minimize the number of logic gates required to implement the function.
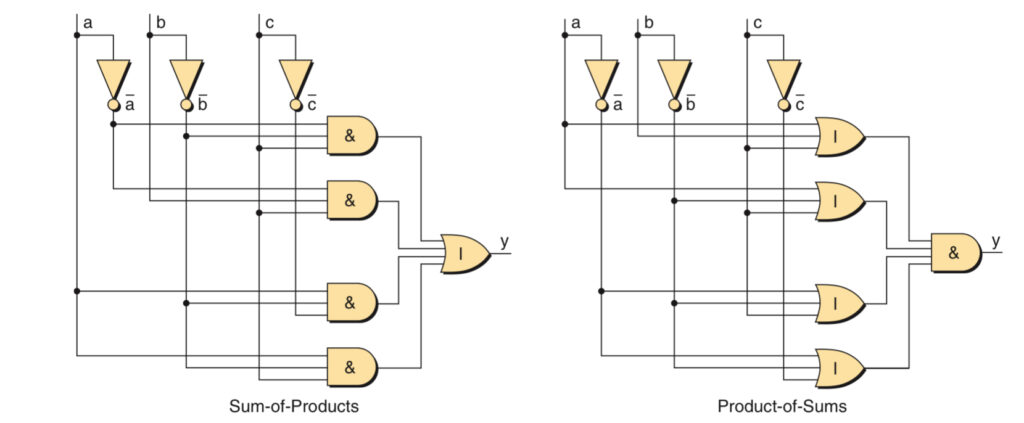
The sum of products and product of sums representations are different canonical forms. Thus, in order to compare two boolean equations, both must be first be coerced into the same canonical form.