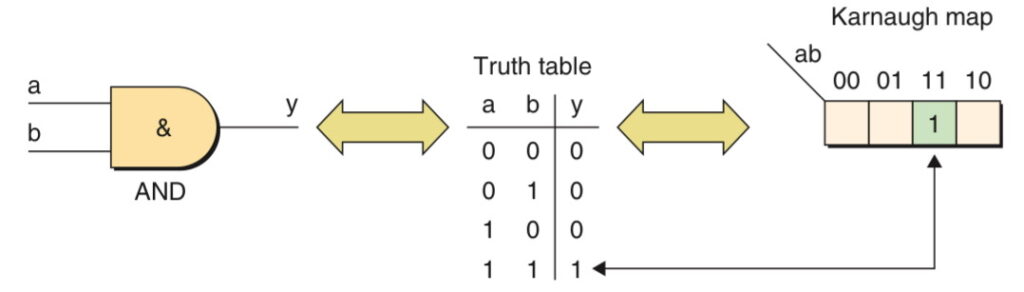
Maurise Karnaugh & Karnaugh Maps
In 1953, American physicist Maurise Karnaugh invented a form of logic diagram called a karnaugh map. The karnaugh map comprises a box for every line in the truth table. The binary values above the boxes are those associated with the inputs. Unlike a truth table, in which the input values typically follow a binary sequence, the Karnaugh map’s input values must be ordered such that the values for adjacent columns vary by only a single bit, this order is known as a Gray code. The y column in the truth table shows all the 0 and 1 values associated with the gate’s output. Similarly, all the output values could be entered into the Karnaugh map’s boxes.
Similar maps can be constructed for 3 or 4 input functions, in the case of a 4 input map, the values associated with the other two inputs must also be ordered as a Gray code.
Minimization Using Karnaugh Maps
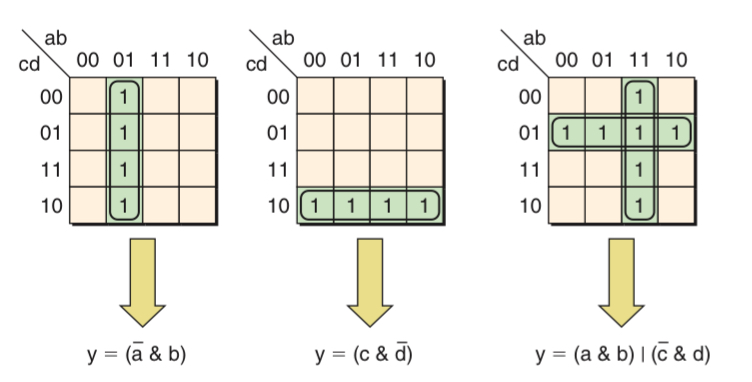
Karnaugh maps are useful in the simplification and minimization of Boolean functions. For example, from a 3-input function truth table, we can get the sum of products containing four minterms. Algebraic simplification techniques could be employed to minimize the equation but it is too time-consuming.
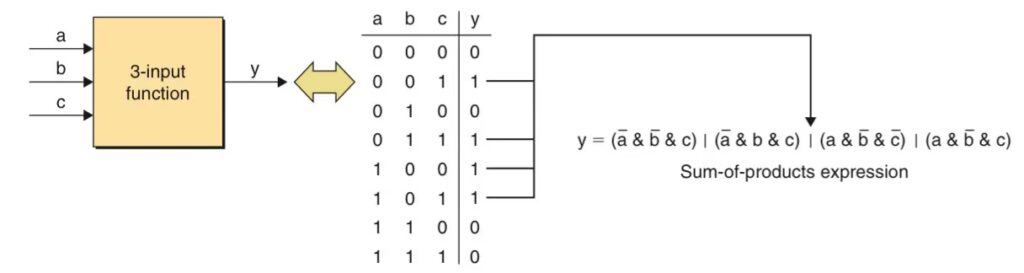
It is when using karnaugh map is a better method. The 1s assigned to the karnaugh maps’ boxes represented the same minterms as the 1s in the truth table’s output column. any pair of horizontally or vertically adjacent boxes corresponds to minterms that differ by only a single variable. Such pairs of minterms can be grouped together and the variable that differed can be discarded, leaving a much simplified equation.
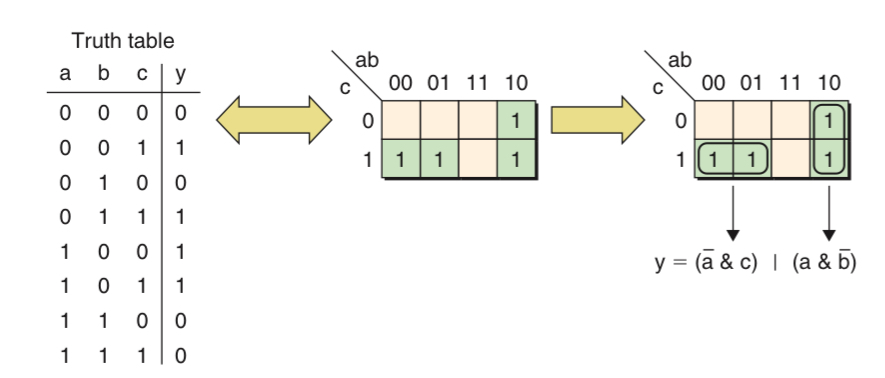
In the case of the horizontal group, input a is 0 for both boxes, input c is 1 for both boxes and input b is 0 for one box and 1 for the other. Thus, for this group, changing the value on b doesn’t affect the value of the output. This means that b is redundant and can be discarded from this group.
Grouping Minterms
Grouping can also be formed from four adjacent minterms, in which case two redundant variable can be discarded. In fact, any group of 2 to the power of n (where n is a positive integer) adjacent minterms can be gathered together.
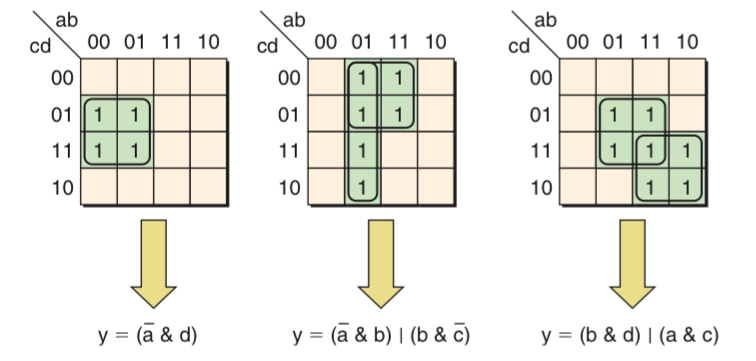
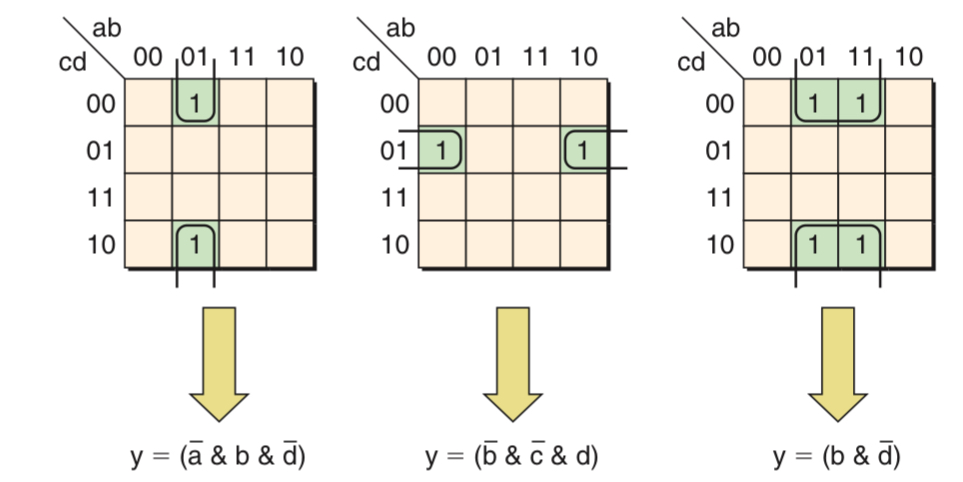
As we know, karnaugh map input values are ordered so that the values associated with adjacent rows and columns differ by only a single bit. One result of this ordering is that the top and bottom rows are also separated by only a single bit, Similarly, the left and right columns are separated by only a single bit as well. This leads to some additional groupings that are not that obvious to find. Moreover, remembering that the left-right columns and the top-bottom rows are logically adjacent, this means that the four corner minterms are also logically adjacent and can form a group too.
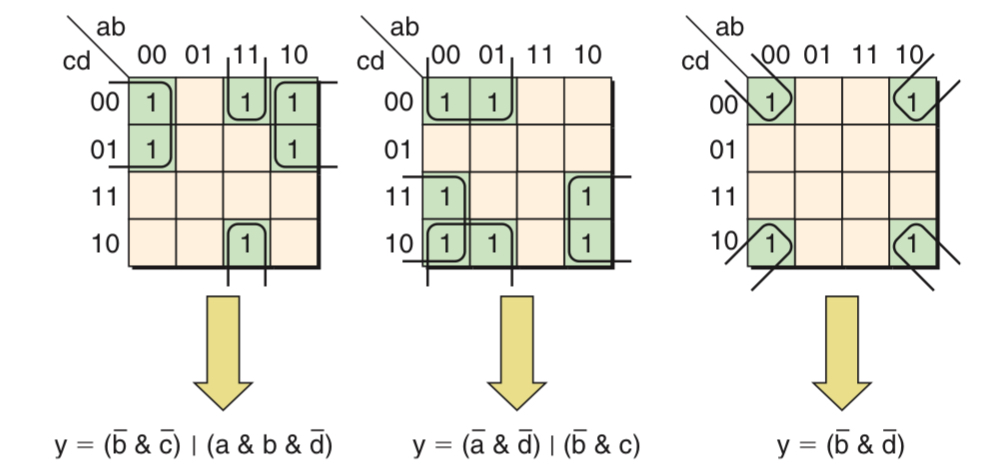
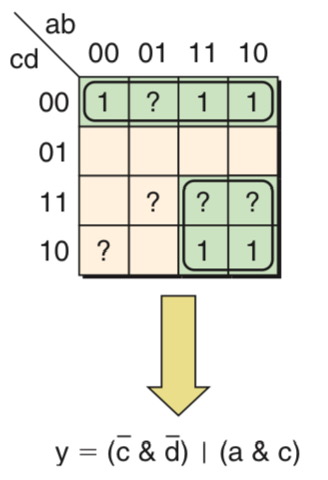
Incompletely Specified Functions
In certain cases a function may be incompletely specified, for example, for some input combinations, the designer may not care about the value of the output. The ? characters indicate that we don’t care about this value of output, which can be considered to represent either 0 or 1 values at the designer’s discretion. In this case, three of the ? character can represent 1 and be used to form larger groups which allows us to minimize the function to a greater degree.
Populating Maps using 0s VS 1s
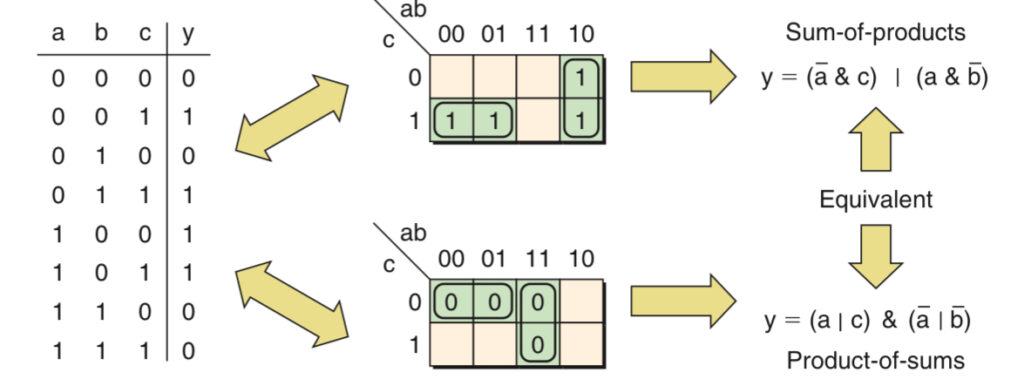
Similar to obtaining logic equations from the truth table, we can use all the 0s from the output or the 1s depending on whether there are fewer 1s or fewer 0s. When a karnaugh map is populated using 1s assigned to the truth table’s output, the resulting boolean expression is extracted from the map in the sum of products form. By comparison, if the karnaugh map is populated using the 0s assigned to the truth table’s output, then the groupings of 0s are used to generate expressions in the product of sums form.
Limitations of Karnaugh graph
Karnaugh maps are most often used to represent 3 input and 4 input functions. It is possible to create similar maps for 5 input and 6 input functions but it becomes difficult to use. It is not considered to have any application for functions with more than six inputs.