Induction

Find the Nth Number in a Sequence

In any sequence, if you know the n^th term rule, you can find any term in that sequence. Remember, n stands for the position of the term: for the 1st term, n = 1; for the 10th term, n = 10; for the 1765th term, n = 1765. We simply substitute n into the n^th term rule for our quadratic sequence.

To find the nth number in a sequence, we first need to find the relationship of the sequence, one of the best ways we can use is induction. The relationship of a sequence in this blog is only limited to linear functions, quadratic functions, cubic functions, and so on. There are several methods that we can use.

First Method: Difference Method:

If we get a series of numbers, we subtract the number on the left from the number on the right. We keep doing this step until the difference between all two numbers is equal.

For example, if the sequence is “3, 7, 13, 21, 31”, find the nth number.

The first difference between each pair of terms is different, but you may notice the differences themselves form a pattern – they go up by two each time

In this case, we repeated the subtraction step two times to get the difference all the same, so this means that this sequence has a quadratic relationship.

What we also notice here is that the difference is 2 in the end. To find the coefficient of n square (n^2), we use the number we get after subtracting which is “2” to divide by 2 which is 1. So the coefficient of n square (n^2) is 2.

After we find that the coefficient of n square is 1, we get that the relationship must be “n^2 + bn + c”. To find b in our case, we need to bring one to five into this formula which is n square, and write one to one above the first to fifth numbers in the sequence. After that, use the number in the sequence to subtract the new number you get. In this case we got “+2, +3, +4, +5, +6”.

Then we subtract two from three, subtract three from four, subtract four from five, and so on. The difference between all equations is 1, so the coefficient of n is “1”

So, now we know that the relationship of the sequence must be “n^2 + n + c”, we only need to find “c”. To find “c” we need to bring one to five into this formula now which is n square plus n (n^2 + n), and write one to one below the first to fifth numbers in the sequence. As you can see, the difference is all “1”. So, the constant is “1”.

At last, the nth number of the sequence is “n^2 + n + 1 (n square plus n plus 1)”.

You might be wondering why, to find the n^th term of a quadratic sequence, we divide the second difference by 2 to find the value of a, when in a linear sequence we can just use the difference itself. The second method to find the n^th term of a quadratic sequence should make this clear.

As we said before, the n^th term rule of any quadratic sequence can be written in the form an² + bn + c. So, let’s substitute the numbers 1 to 5 for n to write out the first 5 terms of the sequence an² + bn + c.

If n = 1, an² + bn + c = a + b + c
If n = 2, an² + bn + c = 4a + 2b + c
If n = 3, an² + bn + c = 9a + 3b + c
If n = 4, an² + bn + c = 16a + 4b + c
If n = 5, an² + bn + c = 25a + 5b + c

This gives us an algebraic quadratic sequence:

a + b + c, 4a + 2b + c, 9a + 3b + c, 16a + 4b + c, 25a + 5b + c

Like any other quadratic sequence, we can find the first and second differences:

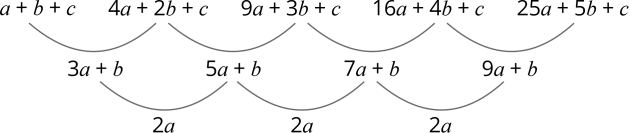
As you can see, the second difference is double the amount of “a”.

Taking the second derivative of a quadratic function, the number obtained is twice the coefficient of the quadratic term of the original formula.

Another way to explain why we need to divide the second difference by two to get the coefficient of x square is by using the derivative.

This is because the derivative of x^2 is 2x, and the derivative of 2x is 2, so the coefficient of x square is 2/2 which is 1.

Using this method, what number should we divide by to get the coefficient of x cube (x^3)?

In this case, we need to find the third derivate, and the answer is that we need to divide the number by 6 in order to find the coefficient of x cube (x^3).

We need to divide 1 in the first difference, divide 2 in the second difference, divide 6 in the third difference and divide 24 in the fourth difference.

We can find a rule that the coefficient of x should be divided by 1, the coefficient of x square should be divided by 1*2, the coefficient of x cube should be divided by 1*2*3, and the coefficient of x to the power of 4 should be divided by 1 *2*3*4, and so on.

Example: find the xth number in the sequence “16, 81, 256, 625, 1296, 2401”