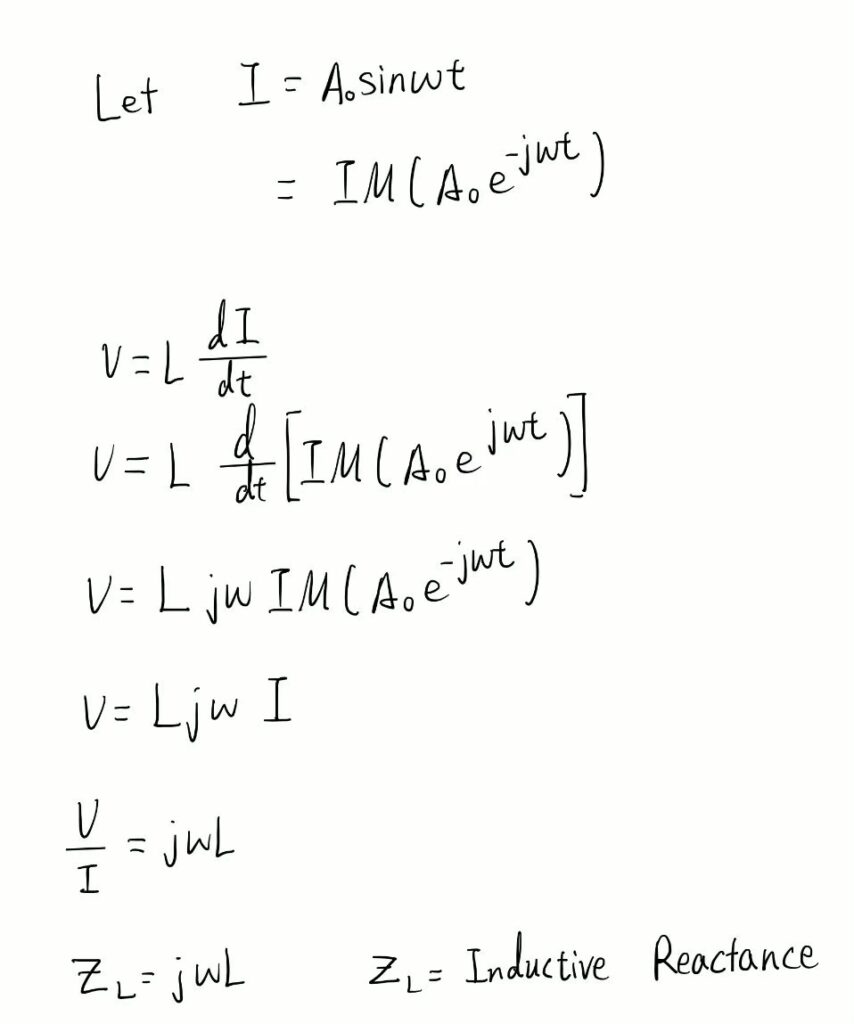Inductors are passive components that store energy through magnetic field. It creates a magnetic field when a current is passed through them.
Inductance is the tendency of electrical conductor to oppose a change in electrical current flowing through it. The current flowing through the inductor cannot mutate because the inductor generates a electromotive force that is opposite to the direction of flow of current which opposes the change of current.

Inductor is represented by the alphabet L and is measured in “Henry”. The formula of inductance is given by the ratio of flux and the current in the circuit. L = Φ/I
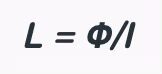
Inductance
A coil is the most recognizable form of an inductor. The inductance of an inductor is linked to a variety of different factors.
- Number of turns
- Coil area
- Coil length
- Permeability of free space
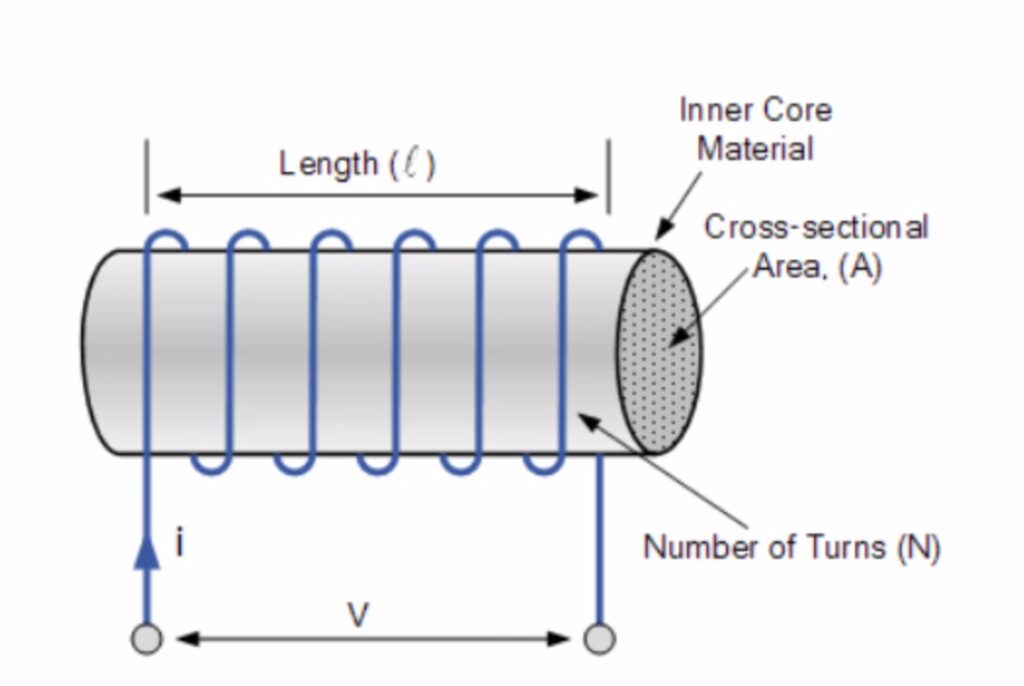
According to Biot Savart Law, the magnetic field at a point due to current carrying element of length l is given by the equation B = (μ₀NI)/L. By substituting the expression for magnetic field B into the equation for magnetic flux, and substituting the expression for magnetic flux into the equation for inductance L, we can find that the inductance is directly proportional to the area of the coil and the square of the number of turns of the coil, and it is inversely proportional to the length of the coil.
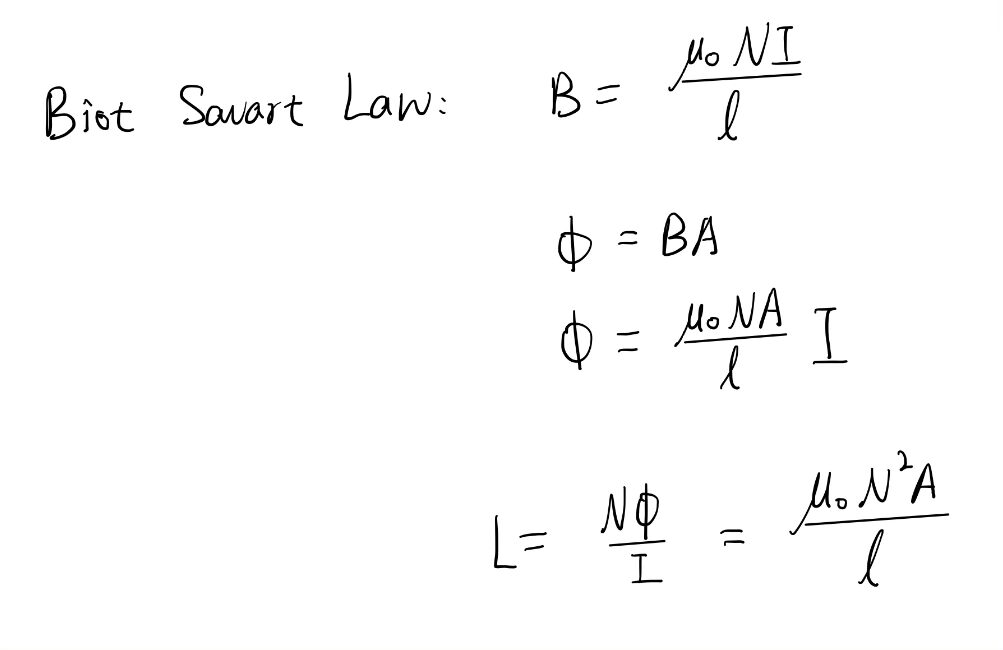
By using Faraday’s law of electromagnetic induction, it can relate the voltage and current across an inductor.
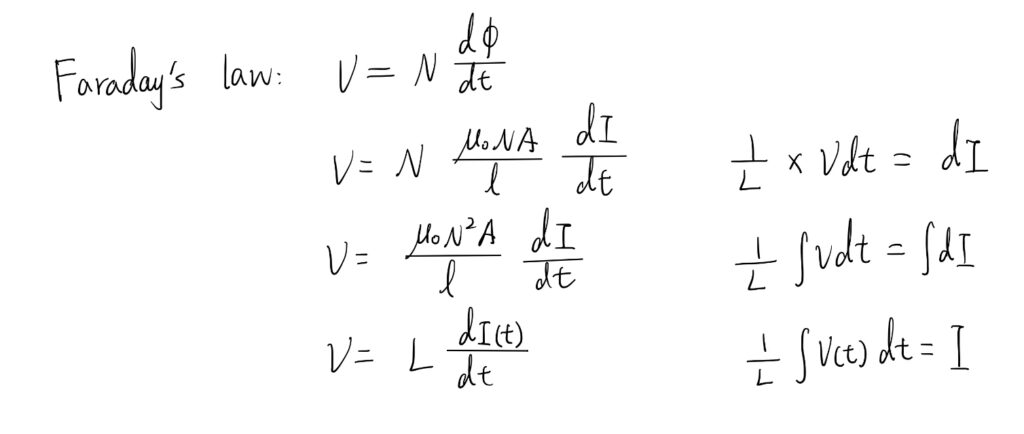
Energy Store in Inductor
An inductor turns electrical energy and stores it as magnetic energy in the form of a magnetic field. The energy stored in a magnetic field is given by the equation E = 1/2 LI^2.
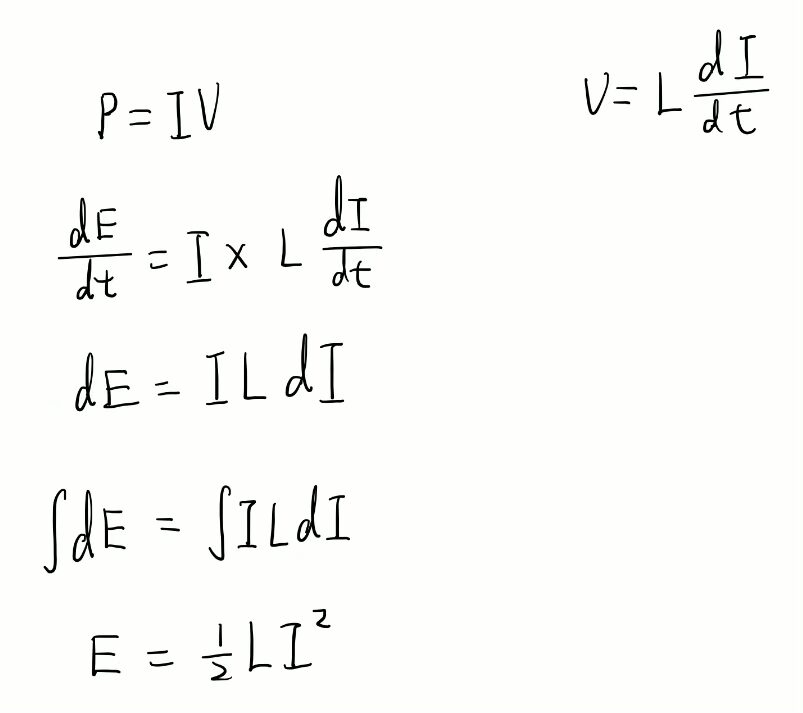
Inductive Reactance
Inductive reactance is the property of an inductor that resists the change in alternating current through it. We assume that the current I through the inductor is periodic and can be expressed using the sine function – Asinωt. We then use the Euler’s formula to express the expression of current. Then, once we substitute the equation of current back into the equation for voltage and do a differentiation, we would find that the inductive reactance is equal to jωL.