Greatest Common Factor:
To find the greatest common factor of two number, you can use a method called short division. Short division is done firstly finding the factors of each number, then the common factors, and finally the greatest common factor among the common factors.
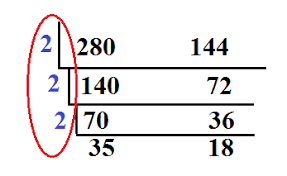
But the problem of short division is: when the common prime factor is small, it can be quickly found by observation; but when the common prime factor is large, it is difficult to find out only by observation. For example, if the greatest common divisor of 1997 and 615 is required, it is difficult to directly find its common prime factor. This method also require too much time to do.
So is there a better way to solve for the greatest common divisor? The answer is yes, which is the Euclidean algorithm to be introduced next.
Euclidean algorithm
You can use Euclid’s algorithm to find the greatest common divisor. Taking the above 1997 and 615 as an example, the Euclidean algorithm is used to solve the following:
1997 / 615 = 3 with remainder 152
615 / 152 = 4 with remainder 7
152 / 7 = 21 with remainder 5
7 / 5 = 1 with remainder 2
5 / 2 = 2 with remainder 1
2 / 1 = 2 with remainder 0
When the remainder is 0, the greatest common divisor of 1997 and 615 is the divisor of the last equation, which in this example is 1.
The above approach is based on the following theorem:
The greatest common divisor of two integers is the greatest common divisor of the smaller of the two numbers and the remainder of the division of the two numbers.
Mathematically expressed as:

Programming this Function
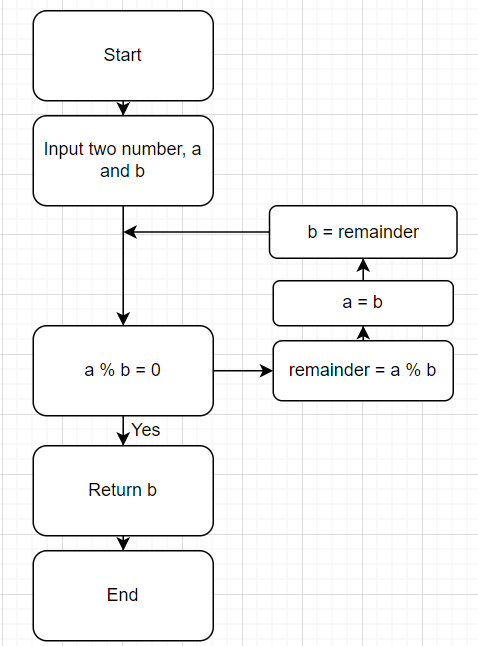
Lowest Common Multiple
To find the lowest common multiple, there are to method to do it, enumeration and the prime factorization method. In enumeration, we list the multiple of the given numbers. The least common multiple is the first common multiple for the given numbers. For 36 and 48, the number 144 is the LCM.
Prime Factorization Method:
- Find the prime factorization of each number.
- Write each number as a product of primes, matching primes vertically when possible.
- Multiplying all the same prime factors together will gives the least common multiple.
However these ways are not fast enough.
To find the least common multiple of two numbers, we need to multiply the two numbers and divide by the greatest common divisor of the two numbers. For example, we need to find the LCM of 12 and 8, we first need to find the GCF of 12 and 8 which is 4. Then we multiply 12 and 8 which is 96 and divide it by 4 which is 24.
One of the drawbacks of this method is that it can only work if we want to find the LCM of two number. It doesn’t work when we need to find the LCM of three or more number. So, we need to repeat this method twice when finding the LCM of three number. For example, we need to find the LCM of 12, 8 and 48 the GCF of the the first two number is 4 and the GCF of all three number is also 4. So, in this case we need to find the LCM of the first two number which is 24 and the LCM of 24 and the third number which is 48. The answer will be 48.
My Python Code
print("This program can find the highest common factor of two numbers.")
a = int(input("Enter your first number: "))
b = int(input("Enter your second number: "))
c = int(input("Enter your third number: "))
def GCF(x, y):
if x < y:
c1 = x
x = y
y = c1
if x % y == 0:
r = y
while x % y != 0:
r = x % y
x = y
y = r
return r
def LCM(x, y):
i = GCF(x, y)
m = int(x * y / i)
return (m)
multiple_ab = LCM(a, b)
factor_ab = GCF(a, b)
print(f"The greatest common factor for the first two number is {factor_ab}.")
print(f"The lowest common multiple for the first two number is {multiple_ab}.")
multiple_abc = LCM(multiple_ab, c)
factor_abc = GCF(factor_ab, c)
print(f"The greatest common factor for all the number is {factor_abc}.")
print(f"The lowest common multiple for all the number is {multiple_abc}.")
Very Good!